Mathematical Olympiad: Mathematics and Youth Magazine, Problem in 412 Issue

Problem in this Issue (Vol 412/10/2011)

FOR LOWER SECONDARY SCHOOLS

T1/412 (For 6 grade). Pick

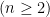numbers $(n\geq 2)$ from th first hundred natural numbers (from 1 to 100) so that the sum of any two distinct numbers is a multiple of 6. What is the largest possible number

so that this can be done?

T2/411 (For 7 grade). Given

$A=\dfrac{5^a}{5^{b+c}}$ and $B=\dfrac{5^a+2011}{5^{b+c}+2011}$

where

are the side lengths of a traingle. Compare

ang

T3/412. Do there exists three integers x,y,z

such that

|x-2005y|+|y-2007z|+|z-2009x|=2011^x+2013^y+2015^z

T4/412. Determine the fllowing sum of 2011 terms

$S=\dfrac{1}{1^4+1^2+1}+\dfrac{2}{2^4+2^2}+\dfrac{3}{3^4+3^2+1}+...+\dfrac{2011}{2011^4+2011^2+1}$

T5/412. Given a circle (O), a chord BC (BC is not a diameter) and point A moving on the major arc BC. Draw a circle (O_1)

passing through B and touches AC at A, another circle (O_2)

passing through C and touches AB at A. (O_1)

meets

at a second point D, different from A. Prove that line AD always passes through a fixed point.

FOR UPPER SECONDARY SCHOOLS

T6/412. A quadrilateral ABCD, with 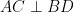$AC\perp BD$ is inscribed in a fixed circle (O,R). Let

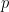be the perimeter of ABCD. Prove that

$\dfrac{AB^2}{p-AB}+\dfrac{BC^2}{p-BC}+\dfrac{CD^2}{p-CD}+\dfrac{DA^2}{p-AD}\geq\dfrac{4R\sqrt{2}}{3}$

T7/412. Slove the system of equations

$\begin{cases}{(17-3x)\sqrt{5-x}+(3y-14)\sqrt{4-y}=0}\\{2\sqrt{2x+y+5}+3\sqrt{3x+2y+11}=x^2+6x+13}\end{cases}$

T8/412. Provw that th following inquality holds of any triangles ABC

$\cos^2\dfrac{A-B}{2}+\cos^2\dfrac{B-C}{2}+\cos^2\dfrac{C-A}{2}\geq 24\sin\dfrac{A}{2}\sin\dfrac{B}{2}\sin\dfrac{C}{2}$

TOWARD MATHEMATICAL OLYMPIAD

T9/412. Two circles (C_1), (C_2)

are given such that the center O of (C_2)

lies on

. Let C, D be their intersection points. Points A and B on (C_1)

and

respectively such that AC touches (C_2)

at C and BC touches (C_1)

at C. The line AB intersects (C_2)

at E and

at F. CE meets (C_1)

at G, GF meets GD at H.
Prove thatGO intersects EH at the circumcenter of triangle DEF.

T10/412. Let a_1,a_2,...,a_n

positive real numbers such that

$a_1^2+a_2^2+...+a_k^2\leq\dfrac{k(2k-1)(2k+1)}{3},\forall k=1,2,..,n.$

Find the largest possible value of the expression

T11/412. Given a sequence (x_n)

such that

$x_n=2n+a\sqrt[3]{8n^3+1},\forall n\in\mathbb{N}^*$

where

is any real number.
a. For what values of

does the sequence has finite limit?
b. Find a such that (x_n)

is eventually increasing.

T12/412. Find all function 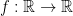$f:\mathbb{R}\to\mathbb{R}$ such that

$f(x^3+y^3)=x^2f(x)+y^2f(y),\forall x,y\in\mathbb{R}.$

Mathematical Olympiad

Saturday, November 26, 2011

Mathematics and Youth Magazine, Problem in 412 Issue

Problem in this Issue (Vol 412/10/2011)

FOR LOWER SECONDARY SCHOOLS

FOR UPPER SECONDARY SCHOOLS

TOWARD MATHEMATICAL OLYMPIAD

No comments:

Post a Comment

Total Pageviews

Mathematics Magazine